√ Pertidaksamaan Linear (Pengertian, Sistem, Soal) – Metropro

Apakah kalian sudah tahu mengenai pertidaksamaan linear? Jika belum, mari kita belajar bersama mengenai pertidaksamaan linear.

Kalian tentu sering mendengar mengenai persamaan. Nah pada artikel kali ini kalian dapat mempelajari materi mengenai pertidaksamaan.

Adapun beberapa pertidaksamaan yang akan qdibahas pada artikel ini adalah pertidaksamaan linear, pertidaksamaan linear satu variabel, sistem pertidaksamaan linear satu variabel, pertidaksamaan linear dua variabel, serta sistem pertidaksamaan linear dua variabel.

Berikut akan dijelaskan mengenai definisi pertidaksamaan linear.

Definisi Pertidaksamaan Linear

Apa yang kalian ketahui mengenia pertidaksamaan linear?

Jika diartikan per kata, pertidaksamaan linear tersusun dari dua kata yaitu “pertidaksamaan” dan “linear”.

Pertidaksamaan merupakan suatu bentuk/kalimat matematis yang memuat tanda lebih dari “ > “, kurang dari “ < “, lebih dari atau sama dengan “ ≥ “, dan kurang dari atau sama dengan “ ≤ “.

Sementara itu, linear dapat diartikan sebagai suatu bentuk aljabar dengan variabel pangkat tertingginya adalah satu. Berikut akan dijelaskan mengenai contoh penerapan pertidaksamaan linear.

Penerapan Pertidaksamaan Linear

Pertidaksamaan linear banyak diterapkan dalam berbagai bidang. Pertidaksamaan linear dimanfaatkan untuk menyelesaikan permasalahan sehari-hari.

Penyelesaian permasalahan dengan menggunakan pertidaksamaan linear dapat dilakukan dengan mengubah permasalahan tersebut ke dalam bentuk model matematika.

Setelah terbentuk model matematika, kalian dapat menyelesaikan model matematika yang kalian buat untuk menentukan solusi dari permasalahan tersebut.

Berikut akan dijelaskan mengenai pertidaksamaan linear satu variabel.

Baca juga Vektor.

Pertidaksamaan Linear Satu Variabel

Pada bagian sebelumnya kalian telah mempelajari mengenai pertidaksamaan linear. Pada bagian ini kalian akan mempelajari mengenai pertidaksamaan linear satu variabel.

Apakah kalian tahu apa itu pertidaksamaan linear satu variabel?

Pertidaksamaan linear satu variabel merupakan bentuk pertidaksamaan dengan memuat satu peubah (variabel) dengan pangkat tertingginya adalah satu (linear).

Bentuk umum dari pertidaksamaan linear satu variabel yaitu sebagai berikut.

Selanjutnya akan dibahas mengenai pertidaksamaan linear dua variabel.

Pertidaksamaan Linear Dua Variabel

Pada bagian sebelumnya kalian sudah belajar mengenai pertidaksamaan linear dua variabel. Bagian ini akan membahas mengenai pertidaksamaan linear dua variabel.

Pertidaksamaan linear dua variabel adalah bentuk pertidaksamaan yang memuat dua peubah (variabel) dengan pangkat tertinggi variabel tersebut adalah satu.

Bentuk dari pertidaksamaan linear dua variabel yaitu sebagai berikut.

Bentuk Umum Pertidaksamaan Linear 2 Variabel

ax + by > c

ax + by < c

ax + by ≥ c

ax + by ≤ c

Keterangan:

• x, y : variabel
• a  : koefisien variabel x
• b  : koefisien variabel y
• c   : konstanta
• <, >, ≤, ≥  : tanda pertidaksamaan

Selanjutnya akan dibahas mengenai sistem pertidaksamaan linear.

Sistem Pertidaksamaan Linear

Apakah kalian mengetahui perbedaan dari pertidaksamaan linear dan sistem pertidaksamaan linear? Perbedaan dari keduanya terletak pada banyaknya pertidaksamaan.

Pada sistem pertidaksamaan linear, misalnya pada sistem pertidaksamaan linear dua variabel, terdapat lebih dari satu pertidaksamaan linear dua variabel agar dapat dibuat model matematika dan ditentukan solusinya.

Pembahasan pada bagian berikutnya akan menjelaskan mengenai sistem pertidaksamaan linear dua variabel.

Baca juga Garis dan Sudut.

Sistem Pertidaksamaan Linear Dua Variabel

Seperti disebutkan sebelumnya, sistem pertidaksamaan linear dua variabel memiliki beberapa pertidaksamaan linear dua variabel agar dapat ditentukan solusi dari pertidaksamaan tersebut.

Perhatikan contoh di bawah ini untuk menentukan solusi dari sistem pertidaksamaan linear dua variabel.

Misalkan terdapat sistem pertidaksamaan linear dua variabel sebagsi berikut.

3x + 2y < 8

x + y < 3

Tentukan daerah penyelesaian dari sistem pertidaksamaan linear dua variabel tersebut jika x dan y merupakan bilangan bulat positif.

Pembahasan

Model matematika:

3x + 2y < 8

x + y < 3

Dengan menggunakan grafik, dibuat garis 3x + 2y = 8, kemudian tentukan bagian yang merupakan 3x + 2y < 8.

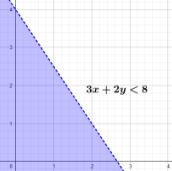
Dengan menggunakan grafik, dibuat garis x + y = 3, kemudian tentukan bagian yang merupakan x + y < 3.

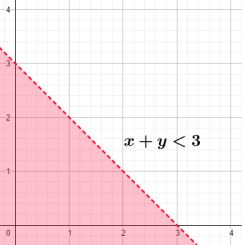
Kemudian tentukan titik potong kedua garis tersebut.

3x + 2y = 8

x + y = 3

Dengan menggunakan metode eliminasi diperoleh:

3x + 2y = 8

2x + 2y = 6

————– –

x   = 2

Substitusikan nilai x = 2 ke persamaan x + y = 3

2 + y = 3

y = 3 – 2

y = 1

Titik potong kedua garis tersebut adalah (2, 1).

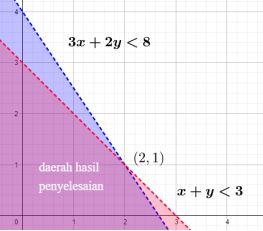
Daerah berwarna ungu merupakan daerah hasil penyelesaian sistem pertidaksamaan linear dua variabel.

Pelajari contoh soal di bawah ini untuk meningkatkan pemahamanmu.

Baca juga Fungsi Komposisi.

Contoh Soal Pertidaksamaan Linear

1. Tentukan solusi pertidaksamaan linear berikut ini untuk nilai variabel merupakan bilangan bulat positif.

Pembahasan

1. 3x < 12

x < 12/3

x < 4

Solusi: {1, 2, 3}

2. 2y > 6

y > 6/2

y > 3

Solusi : {4, 5, 6, . . .}

2. Tentukan daerah penyelesaian dari sistem pertidaksamaan linear dua variabel berikut.

4x + 2 y < 12

2x + 3y < 10

Pembahasan

Buatlah garis 4x + 2y = 12 dan tentukan daerah yang menunjukkan 4x + 2y < 12.

Buatlah garis 2x + 3y = 10 dan tentukan daerah yang menunjukkan 2x + 3y < 10.

Tentukan titik potong kedua garis.

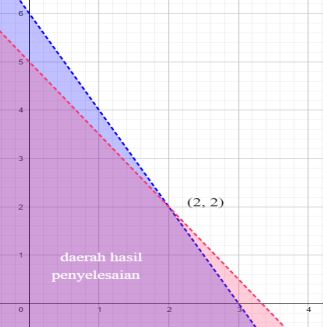
Daerah hasil penyelesaian merupakan daerah yang berwarna ungu.

Mari kita simpulkan bersama.

Kesimpulan

Pertidaksamaan merupakan suatu bentuk/kalimat matematis yang memuat tanda lebih dari “ > “, kurang dari “ < “, lebih dari atau sama dengan “ ≥ “, dan kurang dari atau sama dengan “ ≤ “. Sementara itu, linear dapat diartikan sebagai suatu bentuk aljabar dengan variabel pangkat tertingginya adalah satu.

Pertidaksamaan linear satu variabel merupakan bentuk pertidaksamaan dengan memuat satu peubah (variabel) dengan pangkat tertingginya adalah satu (linear).

Pertidaksamaan linear dua variabel adalah bentuk pertidaksamaan yang memuat dua peubah (variabel) dengan pangkat tertinggi variabel tersebut adalah satu.

Pada sistem pertidaksamaan linear dua variabel, terdapat lebih dari satu pertidaksamaan linear dua variabel agar dapat dibuat model matematika dan ditentukan solusinya.

Demikian penjelasan mengenai pertidaksamaan linear. Terima kasih. Baca juga Segi Empat.