Bahan, jenis dan contoh pertidaksamaan rasional – Metropro

Bahan, jenis dan contoh ketidaksetaraan rasional – Hallo para pengguna artikel rumrumus.com sudah siap untuk melanjutkan pembahasan dengan materi, jenis dan contoh pertidaksamaan rasional? beserta cara mengatasinya? Jangan khawatir semua yang Anda butuhkan ada di sini. Agar tidak bingung mari kita simak pembahasan pertidaksamaan rasional secara detail dibawah ini.

Definisi ketimpangan rasional

Perhatikan setiap bentuk pertidaksamaan berikut.

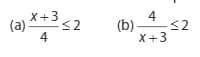
Kedua bentuk pertidaksamaan di atas termasuk bentuk pecahan atau yang dikenal dengan istilah “rasional”. Namun, apakah kedua bentuk tersebut termasuk dalam kategori ketimpangan rasional? Tidak, hanya bentuk (b) yang merupakan pertidaksamaan rasional karena mengandung variabel dalam penyebutnya. Dimana (a) bukan merupakan bentuk pertidaksamaan rasional karena penyebutnya tidak memuat variabel.

Dapat disimpulkan bahwa pertidaksamaan rasional adalah pertidaksamaan dalam bentuk pecahan atau rasional, dimana penyebutnya mengandung variabel.

Jenis ketidaksetaraan rasional

Tahukah Anda bahwa ketimpangan rasional ini dapat dibagi menjadi dua bentuk, yaitu ketimpangan rasional linier bersama pertidaksamaan rasional kuadrat. Bentuk umum dari kedua pertidaksamaan ini adalah sebagai berikut:

1. Pertidaksamaan rasional linier

2. Ketimpangan rasional kuadrat

Sifat ketidaksetaraan rasional

Apakah Anda ingat semua sifat pembagian bilangan bulat ini? Agar Anda ingat kembali, perhatikan ciri-ciri berikut ini:

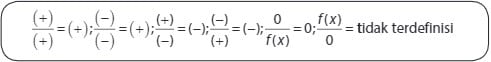
Berdasarkan sifat-sifat distribusi yang dijelaskan di atas, dapat diperoleh ciri-ciri pertidaksamaan rasional sebagai berikut:

Ditetapkan g(x) ≠ 0, sehingga dapat diperoleh sifat-sifat sebagai berikut:

Dengan cara ini, properti berikut dapat diperoleh:

Langkah-langkah untuk penyelesaian

Setelah Anda mengetahui pengertian, jenis, dan sifat-sifat yang dijelaskan di atas, berikut adalah langkah-langkah untuk menyelesaikan pertidaksamaan rasional atau pertidaksamaan pecahan, jadi lihatlah sehingga Anda dapat menyelesaikan masalah dengan mudah dengan teknik ini:

A. Langkah pertama adalah memindahkan semua suku ke satu ruas, misalnya kita ambil ruas kiri sehingga tidak ada suku yang tersisa, berarti ruas kanannya ada nol. Sangat penting untuk diperhatikan, jika kita dilarang untuk mengalikan (x) penyebut silang dan pembilang antara ruas-ruas tersebut. Mengapa begitu dilarang? Karena nilai yang tidak diketahui dapat mengubah bentuk pertidaksamaan saat kita melakukan perkalian silang.

B. Langkah kedua, melakukan operasi aljabar. Apakah Anda pernah mengetahui tentang operasi Jabar ini? Ya, tujuannya biasanya untuk mendapatkan atau mendapatkan bentuk yang lebih sederhana, lalu Anda melakukan pemfaktoran yang dapat difaktorkan untuk mendapatkan atau mendapatkan nilai x.

C. Langkah terakhir adalah menyusun nilai x ke dalam garis bilangan yang ada. Bagaimana dengan ketidaksetaraan kekuatan tinggi dan besar, pertama-tama tentukan tanda-tanda yang disertakan dan buat masing-masing wilayah secara manual. Caranya adalah dengan mengambil nilai x pada luasan kemudian menguji hasilnya terhadap bentuk pertidaksamaan yang ada.

Contoh soal dan cara menjawabnya

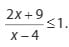
1. Tentukan cara menyelesaikan pertidaksamaan di sebelah -> ini

Berikut cara mengatasinya:
Langkah pertama adalah menyatakan pertidaksamaan di atas dalam bentuk umumnya sebagai berikut:

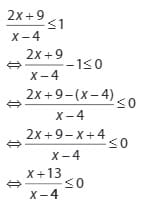
Karena hasil dari langkah awal pertidaksamaan adalah negatif atau sama dengan nol, berlaku hal berikut:

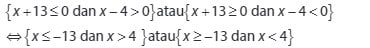
Setelah menentukan irisan-irisan pada luasan, maka diperoleh bentuk sebagai berikut:

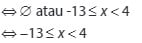
Dapat disimpulkan dari hasil penyelesaian yang diperoleh dari pertidaksamaan pada soal pertama adalah -13 ≤ x < 4.

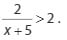
2. Tentukan cara menyelesaikan pertidaksamaan di sebelah -> ini

Berikut cara mengatasinya:
Langkah pertama adalah menyatakan pertidaksamaan di atas dalam bentuk umum sebagai berikut

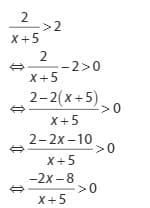
Karena hasil dari langkah pertama pertidaksamaan sudah merupakan hasil positif atau bukan nol, berlaku hal berikut:

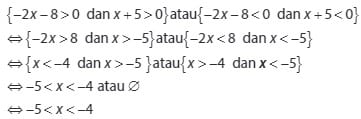
Dapat disimpulkan dari hasil penyelesaian yang diperoleh dari pertidaksamaan pada soal kedua ini adalah -5 < x < -4.

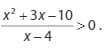
3. Tentukan cara menyelesaikan pertidaksamaan di sebelah -> ini

Berikut cara mengatasinya:

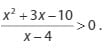
Karena sudah diketahui bahwa pertidaksamaan pada Contoh 3 memiliki hasil positif atau bukan nol, berlaku hal berikut:

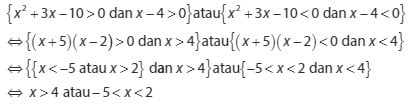
Dapat disimpulkan dari hasil penyelesaian yang diperoleh dari pertidaksamaan pada soal ketiga ini adalah -5 < x < 2 oder x > 4

Demikian pembahasan artikel ini, semoga bermanfaat dan memberikan pengetahuan baru bagi para pembaca.

Baca juga artikel lainnya :