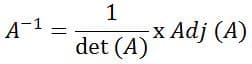Invers Matriks 2×2 dan 3×3 Dengan contoh soal – Metropro

Invers Matriks – Matriks merupakan salah satu bahan ajar matematika yang terdiri dari susunan bilangan dalam tanda kurung. Sedangkan menurut pendapat para ahli, matriks diartikan sebagai rangkaian bilangan yang tersusun dalam baris atau kolom dan tanda kurung siku atau tanda kurung biasa.

Bahan matriks dibagi menjadi beberapa jenis seperti menentukan matriks matriks invers, matriks adjacency, dll. Namun diantara semua jenis materi pada matriks, ada satu materi yang banyak diminati yaitu rumus invers matriks dan contoh soal invers matriks.

Bahkan kita dapat menemukan materi yang memuat rumus matriks atau perkalian matriks dalam matematika sekolah menengah. Kenyataannya masih banyak siswa yang kesulitan mempelajari rumus matriks.

Penggunaan kata invers pada matriks invers yang sama sering dijumpai pada aljabar artinya kebalikan.

Oleh karena itu, kebalikan dari 3 adalah 1/3, jadi kebalikan dari bilangan rasional a adalah 1/a. Hal ini tentu saja juga berlaku untuk matriks.

Namun, dalam matriks ada rumus tersendiri untuk menghitung invers. Rumus invers dapat dibagi menjadi dua jenis, yaitu rumus untuk orde 2×2 dan rumus untuk ordo 3×3.

Pada artikel kali ini, saya akan menjelaskan invers matriks berorde 2×2 dan 3×3 beserta contoh soal inversnya.

Ini ulasan lainnya.

Rumus matriks invers dengan contoh soal

Kami menemukan contoh soal seperti perkalian matriks invers 3 × 3 atau matriks invers 2 × 2 dari matriks invers 4 × 4.

Sebenarnya cara dan cara penyelesaian soal matriks tidak jauh berbeda sampai Anda memahami rumus invers matriks itu sendiri. Jadi bagaimana kita bisa dengan cepat mempelajari rumus matriks?

Kebalikan dari matriks ditampilkan dengan nama depan sebagai huruf besar dan dengan demikian meningkat menjadi -1.

Misalnya, sebagai matriks B, invers dari matriks B & supmin; ¹ ditulis. Sebelumnya kita bahas rumus matriks invers 2×2 dan susun 3×3 beserta contoh soal invers matriks.

Saya akan membagikan beberapa karakteristik inversi. Sifat-sifat matriks terbalik adalah sebagai berikut:

• AA‾¹ = A‾¹A = I
• AB‾¹ = B‾¹A‾¹
• (A‾¹)‾¹ = A
• Jika XA = B, maka X = BA-¹
• Jika AX = b, maka X = A-¹B

Secara umum, rumus invers matriks dapat ditulis sebagai berikut:

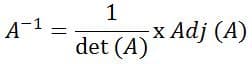
Informasi:

• A‾¹ = invers matriks (A)
• detik (A) = determinan matriks (A)
• Adj (A) = matriks adjoin (A)

1. Matriks invers 2 × 2

Setelah menjelaskan rumus matriks invers dan sifat-sifatnya di atas. Selanjutnya saya akan menjelaskan cara mencari invers dari matriks 2×2.

Tentu saja Anda dapat menemukan invers 2 × 2 menggunakan rumus di atas dan ketika Anda membuatnya lebih mudah daripada matriks pengurutan 3 × 3.

Untuk perhitungan terbalik ini 2 × 2 sesuai dengan metode cepat. Namun, cara cepat ini hanya bisa dilakukan jika urutannya 2×2.

Sebelum itu, kita harus terlebih dahulu mencari nilai matriks adjacency. Lebih jelasnya dapat dilihat pada contoh berikut.

[su_box title=”Contoh Soal Matriks 2×2″ box_color=”#0031e8″]

Temukan matriks invers dari!

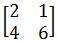
Menjawab:

Untuk menghitung kebalikan dari matriks, metode cepat digunakan. Sebelum menggunakan rumus matriks invers di atas. Pertama, kita perlu mencari nilai adjoin terlebih dahulu.

Untuk mencari matriks invers 2 × 2 yang bertetangga, kita hanya perlu menukar atau memindahkan elemen baris pertama kolom pertama dengan elemen baris kedua kolom kedua.

Selanjutnya, baris kedua kolom pertama dan baris pertama kolom kedua dikalikan dengan -1. Hasilnya adalah sebagai berikut.

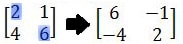
Selanjutnya, cari determinan matriks tersebut
detik = (2 × 6) – (4 × 1)
= 12-4
= 8

Setelah nilai adjoin dan determinan matriks diketahui. Kemudian masukkan rumus matriks di atas. Hasilnya adalah:

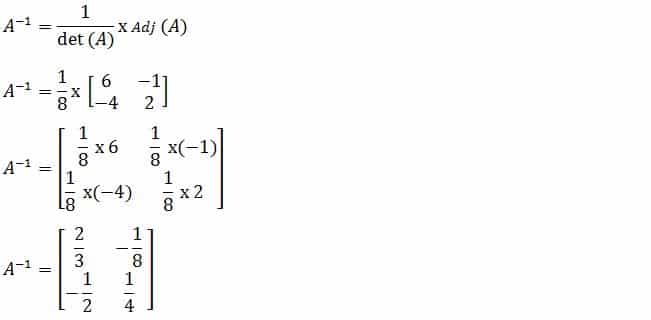
[/su_box]

2. Matriks invers 3×3

Rumus invers dari matriks 3 × 3 sesuai dengan urutan 2 × 2 sebagai berikut:

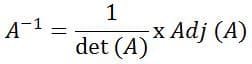
Sama seperti dalam pencarian perkalian matriks 2×2 di atas, kita harus mencari determinan terlebih dahulu untuk mencari invers matriks 3×3. Penspesifikasi urutan 3 × 3 dapat ditemukan dengan dua metode:

1. metode sarrus
2. Metode Kecil – Kofaktor

Secara umum, determinan invers matriks 3×3 lebih mudah dihitung menggunakan metode Sarrus. Metodenya adalah sebagai berikut:

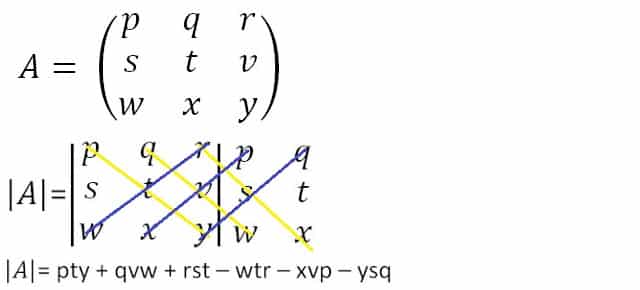
Selanjutnya, kami mencari matriks adjacency dalam rumus matriks invers. Untuk menghitung matriks adjacency, pertama-tama kita harus menentukan nilai matriks kofaktor.

Matriks kofaktor adalah matriks yang elemennya diubah oleh nilai determinan yang nilainya bukan kolom dan tidak sejajar dengan elemen sumber.

Kemudian, sebagai alternatif, diberikan tanda positif atau negatif sebagai berikut:

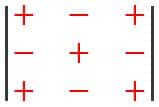
Agar kamu lebih memahami rumus invers matriks 3×3. Saya akan memberikan contoh soal yang berkaitan dengan rumus invers ini. Berikut adalah contoh soal matriks invers.

[su_box title=”Contoh Soal Matriks 3×3″ box_color=”#0031e8″]

Sebuah matriks dikenal sebagai:

Tentukan kebalikan dari matriks di atas A!

Menjawab:

[/su_box]

Demikian penjelasan tentang rumus matriks invers dan contoh soal invers matriks yang dapat saya jelaskan pada artikel kali ini.

Sebenarnya, mengerjakan berbagai soal matriks sangatlah mudah. Kita membutuhkan latihan yang lebih praktis dalam menghafal setiap rumus perkalian matriks.

Hal lain yang perlu kita ingat adalah menemukan produk dari matriks invers.

Kita perlu mencari determinan dan matriks adjoint. Ini adalah rumus matriks invers mutlak.

Baca juga: