Korelasi adalah – Definisi, Rumus Korelasi Berganda dan Parsial – Metropro

Rumusrumus.com kali ini kita akan membahas pengertian dan rumus korelasi serta bentuk hubungan kedua variabel beserta penjelasan tentang rumus korelasi berganda dan korelasi parsial, untuk lebih jelasnya mengenai korelasi simak penjelasan dibawah ini.

Definisi korelasi

Korelasi atau biasa disebut koefisien korelasi adalah suatu nilai yang menunjukkan kekuatan dan arah hubungan linier antara dua variabel acak

Korelasi sederhana adalah teknik statistik yang digunakan untuk mengukur kekuatan hubungan antara 2 variabel dan juga untuk mengetahui bentuk hubungan antara 2 variabel dengan hasil kuantitatif.

Rumus korelasi

Koefisien korelasi sederhana biasa disebut dengan koefisien korelasi Pearson karena memiliki rumus perhitungan koefisien korelasi sederhana yang berasal dari Karl Pearson, seorang ahli matematika dari Inggris. (Rumus ini juga disebut momen produk Pearson)

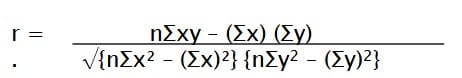
Deskripsi rumus:
N adalah jumlah pasangan data X dan Y
Σx adalah jumlah total variabel X
Σy adalah jumlah total variabel Y
Σx2 adalah kuadrat dari jumlah total variabel X
Σy2 adalah kuadrat dari jumlah total variabel Y
Σxy adalah hasil perkalian dari jumlah total
variabel X dan variabel Y

Bentuk Hubungan Antara 2 Variabel

Korelasi linier positif (+1)

• Perubahan nilai variabel diikuti dengan perubahan nilai variabel lain secara teratur dengan arah yang sama. Ketika nilai variabel X meningkat, variabel Y juga meningkat. Jika nilai variabel X mengalami penurunan, maka variabel Y juga mengalami penurunan.
• Jika nilai koefisien korelasi mendekati +1 (positif), berarti pasangan data X dan Y memiliki korelasi linier positif yang kuat.

Korelasi linier negatif (-1)

• Perubahan nilai variabel diikuti dengan perubahan nilai variabel lainnya secara teratur namun berlawanan arah. Jika nilai variabel X meningkat, maka variabel Y akan menurun. Jika nilai variabel X menurun, maka nilai variabel Y meningkat.
• Jika nilai koefisien korelasi mendekati -1, hal ini menunjukkan bahwa pasangan data variabel X dan variabel Y memiliki korelasi linier negatif yang kuat/dekat.

Tidak berkorelasi (0)

• Peningkatan nilai variabel lain kadang diikuti dengan penurunan pada variabel lain atau kadang dengan kenaikan pada variabel lain.Arah hubungannya tidak beraturan, searah, dan kadang berlawanan.
• Jika nilai koefisien korelasi mendekati 0 (nol), berarti pasangan data variabel X dan Y memiliki korelasi yang sangat lemah atau tidak mungkin berkorelasi.

Koefisien korelasi non-parametrik

Koefisien korelasi Pearson adalah statistik parametrik, dan tidak menggambarkan korelasi dengan baik jika asumsi dasar normalitas data dilanggar. Metode korelasi non-parametrik seperti ρ Spearman dkk T Kendall berguna saat distribusi tidak normal.

Koefisien korelasi non parametrik masih belum cukup kuat dibandingkan dengan metode parametrik jika asumsi normalitas data terpenuhi, namun cenderung menghasilkan hasil yang terdistorsi jika asumsi ini tidak terpenuhi.

Korelasi berganda

Korelasi Berganda (Multiple Correlation) adalah angka yang menunjukkan arah dan kekuatan hubungan antara dua variabel secara bersama-sama atau lebih dengan variabel lainnya. Pengertian korelasi ganda dapat dilihat pada gambar berikut. Simbol untuk korelasi berganda adalah R

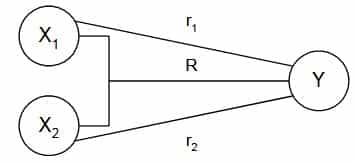Keterangan:
X1 = bimbingan
X2 = tata ruang kantor
Y = kepuasan kerja
R = korelasi berganda

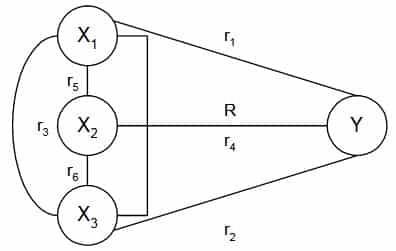Keterangan:
X1 = Kesejahteraan karyawan
X2 = Hubungan dengan kepemimpinan
X3 = pengawasan
Y = efisiensi kerja

Dari contoh di atas terlihat bahwa korelasi berganda R, bukanlah penjumlahan dari korelasi sederhana yang ada pada masing-masing variabel (r1-r2-r3). Jadi R (r1+ r2+ r3).

Korelasi ganda adalah hubungan umum antara X1 dan X2 serta Xn dan Y. Pada gambar pertama. Korelasi berganda merupakan hubungan umum antara variabel kepemimpinan, dan tata ruang kantor dengan kepuasan kerja karyawan

Kopula dan korelasi

Banyak yang keliru menganggap bahwa informasi koefisien korelasi cukup untuk menentukan struktur ketergantungan antara variabel acak.

Untuk menentukan ketergantungan antara variabel acak, kita perlu mempertimbangkan kopula antara keduanya. Koefisien korelasi hanya dapat didefinisikan sebagai struktur ketergantungan dalam beberapa kasus, misalnya pada fungsi distribusi kumulatif dan distribusi normal multivariat.

Korelasi parsial

Analisis korelasi parsial digunakan untuk mengetahui hubungan antara dua variabel, dimana variabel lain yang dianggap berpengaruh dikendalikan atau ditetapkan sebagai variabel kontrol.

Nilai korelasi (r) berkisar antara 1 sampai -1, nilai mendekati 1 atau -1 berarti hubungan kedua variabel semakin kuat, sebaliknya jika nilainya mendekati 0 berarti hubungan kedua variabel . lebih lemah.

Nilai positif menunjukkan hubungan searah (X bertambah dan Y bertambah) dan nilai negatif menunjukkan hubungan berbanding terbalik (X bertambah dan Y berkurang). Data yang digunakan biasanya berskala interval atau rasio.

Pedoman untuk memberikan interpretasi koefisien korelasi adalah sebagai berikut:

0,00 – 0,199 = sangat rendah
0,20 – 0,399 = rendah
0,40 – 0,599 = sedang
0,60 – 0,799 = kuat
0,80 – 1,000 = sangat kuat

Demikian artikel ini, semoga bermanfaat

Baca juga: