Relasi matematika dan sifat-sifatnya, jenis dan contoh soal – Metropro

Rumusrumus.com kali ini kita akan membahas hubungan matematika dan penjelasan tentang berbagai jenis hubungan matematika dan juga akan membahas perbedaan hubungan matematika dan fungsi serta contoh masalah hubungan.

Definisi hubungan

hubungan yaitu Hubungan antara anggota suatu himpunan dengan anggota himpunan lainnya. Hubungan himpunan A dengan himpunan B adalah menghubungkan anggota himpunan A dengan anggota himpunan B.

Bagaimana menjelaskan suatu hubungan

Hubungan antara dua himpunan A dan himpunan B dapat dinyatakan dalam 3 cara, yaitu:

1. Diagram panah
2. diagram kartesius
3. Himpunan pasangan terurut.

1. Bagan panah

Anggota himpunan P berhubungan dengan anggota himpunan Q dengan hubungan “suka”. Itu ditunjukkan oleh arah panah. Itulah sebabnya diagram ini disebut diagram panah.

Contoh:

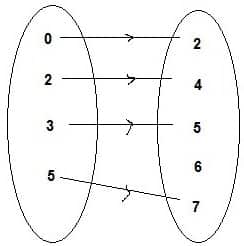
2. Diagram Kartesius

Diagram Cartesian adalah diagram yang terdiri dari sumbu X dan sumbu Y. Pada diagram Cartesian, anggota frase P berada pada sumbu X, sedangkan anggota frase Q berada pada sumbu Y. kalimat P dan Q dilambangkan dengan titik atau periode.

Contoh:

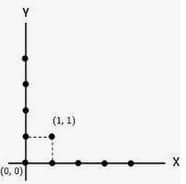
3. Set pasangan yang dipesan

Relasi yang menghubungkan satu himpunan ke himpunan lain dapat disajikan dalam bentuk himpunan pasangan terurut. Cara penulisannya adalah anggota himpunan P ditulis terlebih dahulu, sedangkan anggota himpunan Q menjadi pasangannya.

Contoh:

{(Rani, Basket)}, {(Rani, Badminton)}, {(Dian, Basket)}, {(Dian, Atletik)}, {(Isnie, Senam)}, {(Dila, Basket)}, { ( Dila, tenis meja)}

Properti Hubungan

Suatu relasi A × A, merupakan relasi dari himpunan A ke A saja, memiliki sifat sebagai berikut:

• Refleksif
• Tidak refleksif
• Simetris
• Anti-simetris
• Transitif

Relasi R dari A ke A disebut relasi R dan A.

Jenis hubungan

• Hubungan simetris
• Hubungan anti simetris
• Hubungan transitif
• Hubungan refleksif
• Hubungan terbalik

1. Hubungan terbalik

Misalkan R adalah relasi dari himpunan A ke himpunan B. Kebalikan dari R dinyatakan oleh relasi dari B ke A, yang berisi semua pasangan terurut yang, ketika dipertukarkan, masih termasuk dalam R. Tulis dalam notasi kalimat sebagai berikut; R-1= {(b,a) : (a,b)R}

Contoh:

A = {1,2,3} B = {x,y}
R = {(1,x), (1,y), (3,x)} relasi dari A ke B
R-1= {(x,1), (y,1), (x,3)} relasi terbalik dari B ke A

2. Hubungan simetris

Misalkan R = (A, B, P(x,y)) adalah suatu relasi. R disebut relasi simetris jika setiap (a,b)R memuat (b,a)R. Dengan kata lain, R disebut juga hubungan simetris jika e R b menghasilkan b Ra a.
Contoh hubungan simetris:
jaga satu per satu. Setiap kali Anda menemukan pasangan, misalnya (a,b), cari tahu apakah (b,a) juga ada. Jika tidak ada, hubungannya harus asimetris.

3. Hubungan refleksif

Misalkan R = (A, A, P(x,y)) adalah suatu relasi. R disebut relasi refleksif jika setiap A memuat (a,a)R. Dengan kata lain, R disebut relasi refleksif jika setiap anggota A berelasi dengan dirinya sendiri
Contoh:
Diketahui relasi refleksif A = {1, 2, 3, 4} dan R = {(1,1), (2,3), (3,3), (4,2), (4,4)} adalah R hubungan refleksif? R bukan relasi refleksif, karena (2,2) tidak termasuk dalam R. Jika (2,2) dimasukkan ke dalam R, yaitu R1= {(1,1), (2,2), (2, 3), (3 ,3), (4,2), (4,4) )} maka R1 adalah relasi refleksif.

4. Hubungan anti simetris

Suatu relasi R disebut relasi antisimetrik jika (a,b)R dan (b,a)R maka a=b. Dengan kata lain Jika a, b A, a≠b, maka (a,b)R atau (b,a)R, tetapi tidak keduanya.
Contoh:
Misalkan R adalah relasi dalam himpunan bilangan asli yang didefinisikan sebagai “y habis dibagi x”, maka R adalah relasi antisimetri karena jika b habis dibagi a dan a habis dibagi b, maka a = b.
Misalkan A = {1, 2, 3} dan R1 = {(1,1), (2,1), (2,2), (2,3), (3,2)}, maka R1 tidak antisimetrik relasi, karena (2,3)R1 dan (3,2)R1.

5. Hubungan transitif

Misalkan R suatu relasi dalam himpunan A. R disebut relasi transitif jika ; (a,b)R dan (b,c)R lalu (a,c)R. Dengan kata lain, jika a berhubungan dengan b dan ab berhubungan dengan c, maka a berhubungan dengan c.
Contoh:
Misalkan A = {a,b,c} dan R = {(a,b), (a,c), (b,a), (c,b)}, maka R bukan relasi transitif, karena (b ) ,a)R dan (a,c)R tetapi (b,c)R. diakhiri sehingga R menjadi relasi transitif R = {(a,a), (a,b), (a,c), (b,a), (b,b), (b,c), (c ) a), (c, b), (c, c)}

Perbedaan relasi dan fungsi

Secara sederhana, hubungan dapat diartikan sebagai hubungan. Hubungan yang dimaksud disini adalah hubungan antara daerah asal (domain) dan daerah sahabat (codomain).

Perbedaan antara relasi dan fungsi terletak pada cara menghubungkan anggota himpunan dengan asalnya.

Dalam hubungan, tidak ada aturan khusus untuk memasangkan setiap anggota himpunan asal dengan teman. Aturan hanya terikat oleh pernyataan relasi itu sendiri. Setiap anggota asal daerah dapat memiliki pasangan lebih dari satu atau tidak memiliki pasangan.

Dalam fungsinya, setiap anggota himpunan asal dipasangkan dengan aturan khusus. Aturan ini mensyaratkan bahwa setiap anggota himpunan asal memiliki pasangan dan hanya tepat satu yang dipasangkan dengan daerah pasangan.

Kesimpulannya, setiap relasi belum tentu merupakan fungsi, tetapi setiap fungsi pasti merupakan relasi

Contoh soal hubungan matematika

Contoh soal 1
Himpunan P = {2, 3, 4, 6} dan Q = {1,2,3,4,6,8} dan “faktor dari” adalah relasi yang menghubungkan himpunan P dengan himpunan Q. Atur relasi untuk membentuk himpunan pasangan terurut.

Menjawab:
{(2,2)}, {(2,4)}, {(2,6)}, {(2,8)}, {(3,3)}, {(3,6)}, {( 4,4)}, {(4,8)}, {(6,6)}

Contoh soal 2
kalau siska suka sepak bola, liya suka bola voli dan basket dan berli suka basket dan sepak bola. Tuliskan relasi himpunan pasangan terurut.

Larutan:
{(Siska, sepak bola)}, {(liya, bola voli)}, {(liya, bola basket)}, {(liya, bola basket)}, {(liya, sepak bola)}

Contoh soal 3
Terkenal : Ani suka bakso dan nasi goreng, Irfan suka mie ayam, Arman suka nasi goreng dan coto, Ahmad suka ikan bakar dan Erwin suka bakso. Buatlah diagram panah hubungan

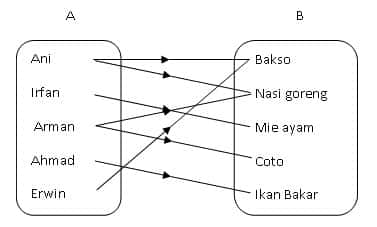Dengan demikian, diskusi tentang hubungan bisa bermanfaat

Artikel terkait: